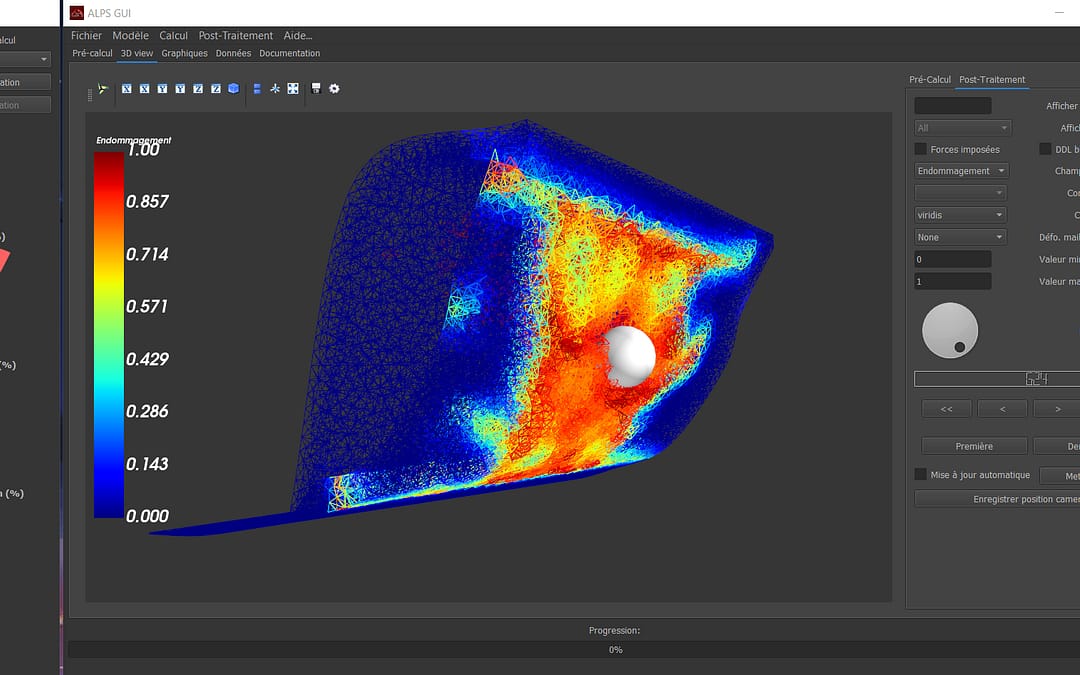
Modélisation d’un impact sur une coque de dériveur en composite grâce à notre outil interne ALPS. La couleur représente le taux d’endommagement ©Ametra Research
La quête d’une meilleure optimisation des structures, souvent liée à des critères écologiques et économiques, pousse à une adoption de plus en plus large des composites dans de nombreux domaines de l’industrie. Réaliser des avions, des trains ou des voitures plus légers permet de réduire leur consommation de carburant de façon significative, optimisant de fait leur coût d’utilisation et leur impact carbone. Ainsi, si cette amélioration incrémentale n’est pas une solution finale au challenge que représente la réponse aux dérèglements climatiques, elle permet de diminuer l’impact carbone des industries du transport le temps de développer une approche permettant de le réduire à zéro (voir ici par exemple).
Les composites sont donc de bons candidats car leurs structures hétérogènes (composées de multiple matériaux) permettent de n’inclure des renforts que là où ils sont absolument nécessaires. Ces renforts se présentent en général sous la forme de tissus et/ou de réseaux de fibres hautes performances (Carbone, Verre, Aramide ou autres) enveloppés dans une résine servant de liant. Ainsi, le béton armé est tout autant un composite qu’une pièce en fibre de carbone et résine époxyde.
L’appellation « matériaux composites » classiquement utilisée par le grand public fait en général référence à un sous-ensemble de ces matériaux composites au sens large : les matériaux composites à matrice organique (CMO). Un CMO est un composite dont le liant est une résine polymère. C’est sur ce type de matériaux qu’Ametra Research travaille dans le cadre du projet ORCA.
Comme explicité ci-dessus, les CMO présentent de nombreux avantages. Il reste encore aujourd’hui beaucoup de questions ouvertes quant à leur utilisation en situation critique et leurs modes d’endommagement. Ces points, sur lesquels les connaissances sont encore limitées, poussent les ingénieurs concevant des structures composites à les sur-dimensionner et à réaliser des campagnes expérimentales extensives et couteuses.
Lorsque l’on travaille sur des matériaux plus « classiques » comme des métaux, ou des plastiques homogènes, il est d’usage de réduire l’échelle des campagnes expérimentales en se servant de logiciels de simulation. Ces campagnes permettent de réduire à la fois les coûts en matière première et en prototypage. Pour effectuer ce type de simulation, la méthode la plus répandue à ce jour dans les bureaux d’étude du monde entier est la méthode des éléments finis (FEM pour Finite Element Method).
Il est courant, dans la nature, de trouver des phénomènes liant une grandeur à son évolution. Par exemple, en admettant qu’une voiture soit partie de Fontenay-aux-Roses à 13h et qu’elle soit arrivée à Orléans à 14h, on peut alors affirmer qu’elle a roulé à 120 kilomètres par heure : on a donc comparé une différence de position de 120km avec une différence d’heures. Si on suppose que l’évolution de la position de la voiture, sa vitesse, était constante pendant le voyage, on peut estimer qu’elle se trouvait à mi-chemin à 13h30. Il est donc possible de calculer la position de la voiture en fonction des différences entre l’endroit et l’heure du départ et d’arrivée. Ce type de calcul faisant intervenir des évolutions de grandeurs physiques est donc appelé un calcul différentiel. Il est important de noter que si la vitesse n’est pas constante au cours du voyage, le calcul est alors bien plus complexe. Le calcul différentiel est à la base de nombreuses équations régissant le comportement des choses qui nous entourent, et le comportement des matériaux ne déroge pas à cette règle.
La FEM est un outil très puissant, car elle repose sur l’idée de découper des problèmes différentiels complexes en une somme de problèmes simples. Malheureusement, cette dernière est intrinsèquement incapable de représenter une apparition d’endommagement sans intervention d’artifices numériques (on vous épargne ici les détails).
Lorsque l’on souhaite dimensionner des pièces fabriquées en CMO, en particulier leurs assemblages, il est fondamental de prendre en compte l’endommagement de ces dernières. En effet, elles ont tendance à s’endommager de façon moins visible et donc plus insidieuse que des pièces classiques. L’affaiblissement voire la rupture complète du lien entre fibre et matrice est par exemple très difficile à observer à l’œil nu, alors qu’il peut être la cause d’une forte dégradation des capacités du composite. Par ailleurs, dans de nombreux cas de chargements accidentels, une pièce en métal va se déformer de façon irréversible longtemps avant d’atteindre la rupture, tandis qu’une pièce en composite sera plus sujette à une rupture soudaine et brutale.
Ainsi, afin d’assurer la sécurité des passagers, des conducteurs, des sportifs ainsi que l’ensemble des utilisateurs de matériaux composites, il est nécessaire de développer de nouvelles approches numériques. Ces dernières se doivent d’être capables de répondre aux problématiques liées à la modélisation de l’endommagement. Elles permettraient de ce fait d’optimiser la conception de ces produits toujours plus innovants.
Nous travaillons donc, au sein d’Ametra Research, au développement et à la validation d’un code de calcul d’une méthode innovante et prometteuse. Cette méthode s’appelle la Péridynamique. Introduite au début des années 2000, elle est basée sur une approche dite particulaire. Ainsi, contrairement à la FEM, elle ne repose pas sur la résolution directe d’équations différentielles. Elle n’est donc pas sujette aux même limites que la FEM, ce qui la rend particulièrement attrayante dans le cadre de la modélisation d’impacts et de ruptures. La péridynamique sera décrite plus en détail dans un article publié prochainement sur notre blog.
Découvrez dès maintenant le site officiel d’Ametra Group et n’hésitez pas à nous suivre sur LinkedIn pour ne rien manquer des actualités du groupe.